こんにちは。伸学会の菊池です。

先日とてもがっかりすることがありました。

算数の授業のときに、以前解説した問題７問の再テストを行ったのです。

その結果、なんとクラスの半数近くの子が、解説を聞く前の最初の点数と変わっていませんでした。

そして残りの子たちのうちの大半は、１～２問は正解が増えたかなという程度。

全問正解できた子は１人だけしかいませんでした。

あの解説は何だったんだろう。。。がっかりしてしまいます。

あなたも、お子さんがもう一度やっても進歩がほとんど見られなかったらそう思ってしまいますよね？

 

でも、本当はそんな風に考えてはいけないんです。

なぜなら、彼らが100％悪いとも言い切れないからです。

だから、難しいことではありますが、私もがっかり感をなるべく出さないように、子供たちを「頑張ろう！」と励ましました。

その再テストの問題は図形問題でした。

中学受験は大雑把に分けると「図形」と「文章題」に分かれます。

そのうちの「図形」が苦手で、何度やってもなかなかできない子ってけっこういます。

特に女の子は苦労することが多いです。

あなたのお子さんはどうですか？

 

なぜなかなか伸びないかというと、その問題を解くための「知識」はあっても「能力」が足りないからです。

そのうちの１つが、図形の中で特定の部分に着目する「目」です。

例えばこういう問題。

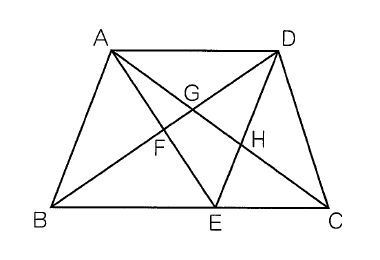
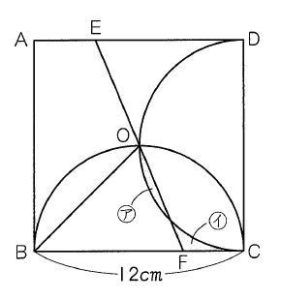
こういう複雑な図形を見たときに、「目」がない子は隠れた相似やおうぎ形をとらえることができません。

解説をするときに色ペンでぬり分けてあげたり、補助線を入れたりすると「ああー！」ってなるのに、自分でそれを見つけようとしてもからっきしダメなんです。

そういう子は、相似やおうぎ形の公式や解き方をわかっているのに、お手上げってなってしまいます。

似たような例だと、私は「立体視」がなかなかできず、平行法とか交差法とか言われてもさっぱりです。

これが立体に見えますと言われても意味がわかりません。

彼らもそんな気持ちなのかと思うと、がっかりしたり怒ったりしちゃいけないなと思うのです。

だって本人は頑張っているのに、かわいそうですよね。

私は立体視ができるようになることに大した魅力は感じないのでできなくても良いのですが、算数の図形問題ができない子たちはそうはいきません。

いったいどうしたら良いのでしょうか？

 

そういう子にはこういう教材から練習をさせなければいけません。

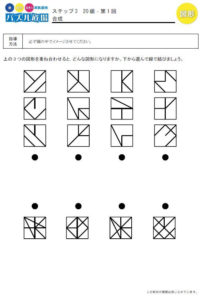
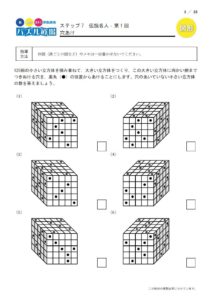
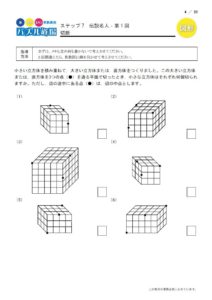
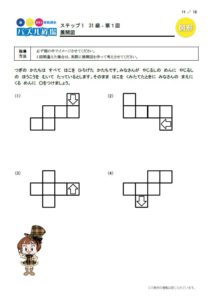
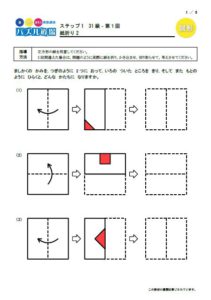
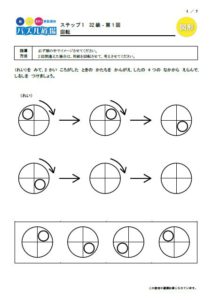
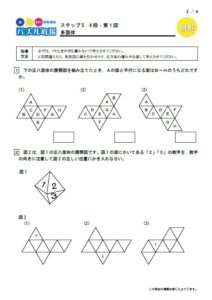
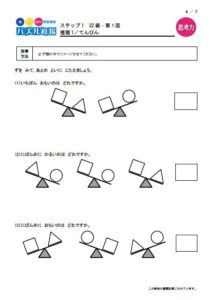
こちらはパズル道場にある図形の合成です。

いくつかの図形を重ね合わせるとどうなるかを考えるパズルですが、完成形から逆に考えることもするので、複合図形の中の一部分を浮かび上がらせて考える訓練になります。

もちろん市販の教材でも同じようなものがあるので、探していただいてもかまいません。

 

なぜこういった教材からやらせなければいけないか？

それは、普通の「算数」の問題は様々な能力がうまくかみ合わないとできないようになっているからです。

よく保護者の方に、「図形問題が苦手だからパズル道場をやらせてください」とお伝えすると、「図形問題が苦手なら図形問題を練習させてください」という返答が返って来ることがあります。

それってバスケットボールがうまくなりたいときに、「とりあえず試合に出して経験積ませてください」って言ってるのと同じですから！

ドリブルの練習・パスの練習・シュートの練習・戦術の勉強・スタミナの強化・ジャンプ力の強化などなど、個別の練習をしなければうまくなるはずありませんよね？

試合でシュートが決められなかった。

じゃあなぜ？と理由を探せば、何かがボトルネックになっているはずなのです。

・戦術の理解が足りないから、シュートを決めやすいポジショニングができていなかったのかもしれない。
・ジャンプ力が足りないから、ブロックに邪魔されやすいのかもしれない。
・スタミナが無いから、終盤になると力が出せないのかもしれない。
・そもそもフリースローなど止まった状態でもシュートが下手だから、めまぐるしく動く試合中はなおさら成功しないのかもしれない。

そういったボトルネックになっている理由を探して、１つ１つ個別の練習をしなければいけません。

それら個別の能力やスキルを身につけた後でようやく、「試合」という「能力やスキルを統合して運用する場」が成長に繋がるようになるのです。

 

算数でも同じです。

平面及び立体の図形の分解力・空間図形の認識力・場合わけの感覚・条件整理の感覚・規則性の感覚・大きさの感覚・割合の感覚・分数の感覚・素因数分解の感覚・計算力、そしてこれらに加えてそれぞれの単元ごとの公式や解法の理解と暗記。

問題を解くために必要なスキルや能力を分解して、足りていないところを１つ１つ練習しなければ、時間の無駄になったり、そもそも練習にならなかったりします。

そのことに気づいておらず、間違った練習法「とにかく問題を解けばいい」を実行させてしまうお父さんお母さんがとても多いです。

あなたはそんな間違いはしていなかったでしょうか？

もう一度確認しておくと、算数の問題を解くには様々な能力をうまくかみ合わせないといけません。

逆に言えば、今その問題ができていないとしたら、何かたった１つがボトルネックになっている可能性もあります。

これまでの生徒でも、そのボトルネックが解消されただけで、一気にいろいろな問題ができるようになった子が何人もいます。

なるほど、お前ここで詰まってたのね、と。

４・５年生の子であればそのボトルネックを解消するために、３年生以下の子であればそもそもそんなボトルネックを作らないために、１つ１つの能力を鍛えるトレーニングをさせてあげてくださいね。

伸学会でも、パズル道場で１つ１つ個別にトレーニングさせています。

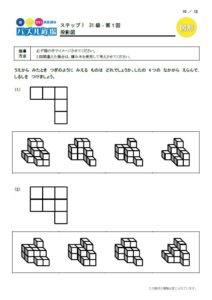
知識と違って、能力は一朝一夕に身につくものではありません。
ですが、低学年のうちから時間をかけてこういったトレーニングをさせれば、必ず能力は成長します。
そして、算数を得意にできます。

算数は受験で最も差がつく科目ですから、ここが得意になれば大きなアドバンテージを稼いで、合格に向けて１歩も２歩もリードができます。

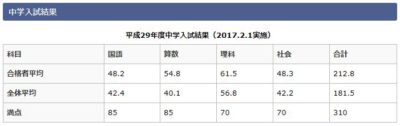
一例として、開成中学校の入試結果。算数だけ他の科目の3倍くらい差がついています。

もちろんそれは中学受験が終わった後の大学受験でも同じです。
理系であればもちろんそこが勝負どころになりますが、文系でも意外と数学が有利に働きます。
数学はできる子とできない子の差が激しく、そして苦手意識がある子の方が圧倒的に多数なので、社会で受験をしようとする子が多くなります。必然的に熾烈な争いになります。
それに対して、数学は選ぶ子が少ないので、社会に比べれば有利な戦いができます。
伸学会のスタッフでも、宮本先生や山崎先生は地歴ではなく数学で受験して慶應大学の経済学部の合格をとっています。
横田先生も同様に、数学受験で早稲田の政経学部に合格しています。

算数は理数の生涯学習の第一歩目。
ここでつまずくか良いスタートを切れるかの差は、先に進むほど大きな差になります。
ここが分かれ道です。
良い方向に行かせてあげれば、あなたのお子さんが将来困る可能性を大きく減らせますよ。

まずはお子さんを算数が得意な子にさせてあげましょう。
そのためには、ボトルネックを作らないこと。
そしてそのためには、必要な能力を個別にトレーニングすること。

ぜひ実践してくださいね。

—
パズル道場の体験会を開催します。
もしあなたも、お子さんに対して
・試行錯誤をして、頭を使う習慣を身につけてほしい
・友達とともに、協力しながら能力を伸ばしていってほしい
・難しい算数の問題を解けるセンスを磨いてほしい
・難しい問題を楽しめるようになってほしい
・算数を得意にして難関校と呼ばれる学校の入試を解けるようになって合格を掴み取ってほしい
・将来にわたって、数学を武器にして社会で活躍する子になってほしい。
・やる気や忍耐力といった非認知スキルを身につけて、将来活躍する子になってほしい
そう思っているのなら、

ぜひ、パズル道場体験会に参加して下さい。
センスを磨くための方法をお子さんに一からお教えしますよ。
お子さんが体験している間には、お父さんお母さんにはパズル道場でどんな問題を先々扱っていくか、それによってどんな能力が身につくか、詳しく説明しますね。

パズル道場の体験会は11月5日(日)に自由が丘校で、11月19日(日)に目黒校で開催します。
時間は11時～12時、14時～15時、16時～17時の３回実施します。
定員は各回６名なので、もしかしたら満席になってしまうかもしれません。
興味がある方は今すぐお申込みお願いします。
↓のボタンをクリックして、申込フォームから都合の良い日時を選んで申し込んで下さい。

よろしくお願いします。

それから、今体験に参加する方には、「パズル道場」のオリジナルシールなどのグッズをプレゼントしています。